Опыты Саньяка
В 1912г. Гаррес, а затем Саньяк выполнили так называемый «вихревой» опыт, идея которого заключалась в том, что луч света разделяется на два, один из которых движется в направлении вращения установки, другой – в противоположном направлении. В опыте Гарреса лучи света движутся внутри кольца, составленного из прозрачных кристаллов; в опыте Саньяка – в воздухе. Схема опыта Саньяка приведена на рис.1.
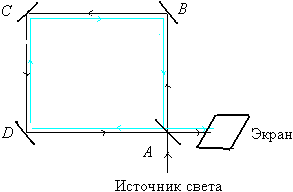
Рис. 1. Схема опыта Саньяка
Луч света попадает на полупрозрачное зеркало A, где расщепляется на два луча. Один луч движется по контуру ABCD, другой – в противоположном направлении.
Когда прибор неподвижен, время, затрачиваемое на обход замкнутого пути ABCD, обратно пропорционально v. Когда прибор вращается, время, затрачиваемое на обход того же контура, обратно пропорционально величине (c+v) для луча света, движущегося в одном направлении, и величине (c–v) для луча света, движущегося в противоположном направлении. Опыт Саньяка был повторен Погани в 1925 .1926гг. Как считает С.И.Вавилов «Маленький интерферометр Саньяка обнаруживает . оптический вихрь», следовательно, он не увлекает эфира. Таково единственно возможное объяснение этого опыта на основе представления об эфире . Если бы явление Саньяка было открыто раньше, чем выяснились результаты опытов второго порядка, оно, конечно, рассматривалось бы как блестящее экспериментальное доказательство наличия эфира. Но в ситуации, создавшейся . после опыта Майкельсона, опыт Саньяка разъяснил немногое» [1], главным образом потому, что эти опыты не были доведены до своего логического завершения. По крайней мере, остался невыясненным главный вопрос: что такое прибор движущийся и прибор неподвижный? Относительно чего измеряется скорость вращения интерферометра в этих опытах?
Можно сказать, что скорость измеряется относительно неподвижного воздуха в лаборатории, где выполнялись эти опыты. Предположим, однако, что опыты выполнятся в вакуумной камере, заполненной воздухом. Предположим, что прибор вращается вместе с вакуумной камерой. Есть основания утверждать, что в этом случае вращение прибора вместе с вакуумной камерой относительно стен лаборатории не будет сопровождаться изменением интерференционной картины, с какой бы скоростью не вращалась вакуумная камера вместе с прибором, поскольку в этом случае отсутствует движение прибора относительно окружающего этот прибор воздуха. Значит, причиной изменения интерференционной картины является движение прибора относительно окружающего прибор воздуха? И действительно, вращение прибора относительно воздуха внутри неподвижной вакуумной камеры приведет к изменению интерференционной картины, соответствующей скорости вращения прибора. Предположим, однако, что в вакуумной камере создан глубокий вакуум. И в этом случае есть основания утверждать, что вращение интерферометра относительно неподвижной вакуумной камеры приведет к изменению интерференционной картины. Очевидно, что вращение прибора относительно стен вакуумной камеры есть одновременно вращение относительно вакуума или эфира, находящегося внутри вакуумной камеры. Следовательно, причиной изменения интерференционной картины является вращение интерферометра относительно вакуума или эфира, неподвижного внутри неподвижной вакуумной камеры. Если бы Саньяк выполнил такой опыт, сегодня ни у кого не было бы сомнений в том, что и в оптике движение относительно эфира всегда сопровождается вполне наблюдаемыми явлениями, соответствующими скорости этого движения.
Предположим, далее, что Саньяк несколько изменил схему своего опыта так, как это изображено на рис.2. Как и прежде, луч света, проходя через полупрозрачное зеркало, расщепляется на два луча, движущихся во взаимно противоположных направлениях к непрозрачным зеркалам S1 и S2, отражаются от этих зеркал и, снова проходя через полупрозрачное зеркало, попадают на экран или в зрительную трубу, где наблюдается интерференционная картина. Прибор вращается относительно оси, проходящей через точку A.
Немного больше о технологиях >>>
Обобщенный принцип наименьшего действия
Введены
континуально многозначные функции, позволяющие адекватно описывать физические
задачи. Показано их отличие от разрывных функций. Сформулирована и решена
вариационная задача для функционалов с разрывным интегрантом, зависящих от
линейных интегральных операторов, действующ ...
Применение гидролокатора бокового обзора для прокладки и контроля положения подводного трубопровода
При эксплуатации подводных участков нефте- и
газопроводов необходимы регулярные технические инспекции для контроля состояния
тела трубы и ее опор. Предлагаемая технология обследования подводного
трубопровода с использованием гидролокатора бокового обзора характеризуется
высокой ...
